The Greater Male Variability Hypothesis (GMVH) suggests that males exhibit greater variance than females in their cognitive abilities. I present some relevant empirical findings and make a suggestion for how the hypothesis should be conceptualized and evaluated.
Introduction
Darwin observed and remarked that males tend to exhibit greater variance than females in their physical characteristics. It has been argued — with a good amount of empirical support — that this also holds true for cognitive abilities among people. That is, the male “bell curve” for cognitive ability is slightly flatter and more spread out than the equivalent female bell curve.
A normal distribution (the familiar “bell curve”) is governed by two parameters; its mean (average) and variance. Sex differences can exist in either of these two parameters. Cohen’s d is often used to quantify a mean difference, and its value represents the average difference in terms of (pooled) standardized units. By convention, a positive value implies that males have greater mean, zero implies that there is no mean difference, and negative values imply that females have greater mean. To quantify differences in variance, we typically use the variance ratio (VR). This is simply calculated by dividing the male variance with the female variance. A variance ratio of 1 thus implies no difference between the groups. Values greater than one imply greater male variance, and values smaller than one imply greater female variance.
I argue that a simple insight helps conceptualize and empirically test the GMVH, as well as clear up seeming “contradictions” to the hypothesis. This is the fact that there is a positive relationship between the mean sex difference and the variance ratio. That is, when d values are larger, VR values also tend to be larger (and vice versa). Then, to suggest that males in general exhibit greater variance means that male variance tends to be greater even when there there is no mean difference.
A quantity, VR₀, is helpful to define here. It is mathematically defined as the expected value of the variance ratio when there is no mean difference, i.e., VR₀ := E[VR | d = 0]. I posit that the GMVH, properly understood, can be reduced to a very simple assertion: VR₀ is greater than one. To make this claim more tangible, we will look at some real empirical data.
CogAT
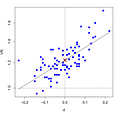
The Cognitive Abilities Test (CogAT) assesses students’ cognitive abilities through a battery of items. Lakin (2013) reports the results of large samples of U.S. students in grades 3-11 (see Table 3 in the paper). The results span 4 cohorts (1984, 1992, 2000, 2011), 3 different tests (verbal, quantitative, and nonverbal), and 7 different grade levels. In total, this gives 84 (4 times 3 times 7) samples where sex differences were assessed, each sample consisting of many students. Previously I suggested that there is a positive relationship between d and VR. This is illustrated in the plot below.
The figure displays the mean difference (in terms of Cohen’s d) on the horizontal axis, and the variance ratio (VR) on the vertical axis (which is logarithmic). It is important to understand that a dot does not represent a single individual, but rather the summary result of the sex difference in one cohort, on a particular subtest, in a particular grade level. For example, one of the dots represents the summary result of the quantitative subtest in the 2011 cohort at the grade level with students aged 11. All dots with d greater than zero (to the right of the vertical dashed line) were tests where males scored higher than females on average. All dots with VR greater than one (above the horizontal dashed line) were tests where males had greater variance than females.
A few findings are notable. Mean differences are small on these tests, generally below 0.2 standard deviations. Male variance is greater than female variance for almost all of them. Importantly however for this discussion: there is a clear positive relationship between d and VR. It is easy to see from visual inspection of the points, but it is also seen from the positive slope regression line (r = 0.71; p < 0.001). The regression line also gives us an estimate of VR₀, as it is simply the regression line’s VR value when d = 0 (i.e., where it crosses the vertical axis). Here VR₀ is estimated as 1.22, illustrated with a red cross symbol. This value is significantly different from 1 (p < 0.001), and therefore supports the GMVH.
Project Talent
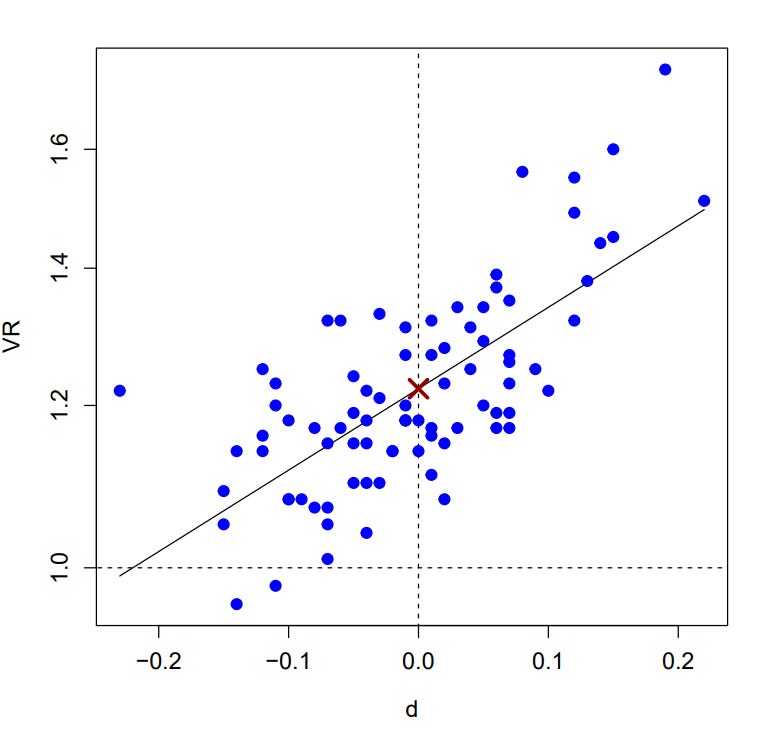
In 1960, a large-scale U.S. nationally representative sample of the 15 year-old age group were cognitively assessed. Project Talent remains one of the largest and most comprehensive studies in U.S. history, subjecting the participants to a highly comprehensive 2-day test battery including various information and aptitude tests. Like before, I illustrate the relationship between d and VR below.
We find a significant positive relationship between d and VR (r = 0.68, p < 0.001), albeit the relationship is more noisy than in the CogAT data. Here VR₀ is estimated as 1.16, and is significantly greater than 1.
National Longitudinal Study of Youth, 1979 (siblings)
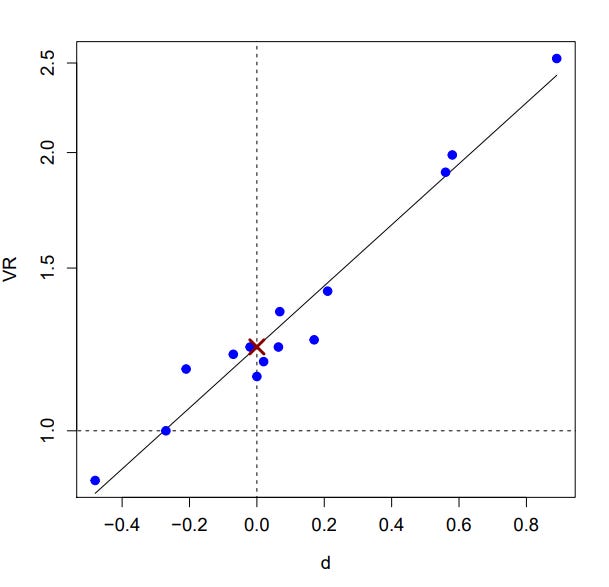
The National Longitudinal Study of Youth (NLSY1979) is another large study which, among many other things, subjects participants to a battery of cognitive and informational tests. Deary et al. (2007) considers the subsample of opposite-sex siblings, which represent great control cases for each other and thus reduces potential systematic sampling error. Like before, I visualize their results below (see Table 1 in the paper).
This battery has fewer subtests, however the relationship is still clear and significant (r = 0.98, p < 0.001). Here VR₀ is estimated as 1.23.
Discussion
Here I have attempted to illustrate two points. First, there is a positive relationship between the magnitude of the mean difference and the magnitude of the variance ratio. This helps solve some of the apparent “contradictions” or “exceptions” to the GMVH. For example, Arden & Plomin (2006) analyze sex differences in cognitive abilities of very young children aged 2 to 10. In all cases except one (age 2), they find that variance is greater among males than females. In this exception, instead of males having higher variance, there was no significant or practical difference in variance. This exception, however, is easily explained by the fact that the females here had a sizeable mean advantage of around 0.4 standard deviations. The relationship between d and VR suggests that when d is negative, VR tends to be smaller. If VR₀ was 1, the variance ratio should be expected to be significantly smaller than 1 when females have such a noticeable mean advantage. The fact that this is not observed is consistent with VR₀ being greater than 1. In that sense, this result is not an exception at all. Indeed, one can repeat the same procedure as in previous sections with Arden & Plomin’s results, and a similar picture emerges. The same is also often observed in other standardized tests where females have a substantial mean advantage, such as reading and writing components of the SAT or PISA tests.
Second, I have suggested that, to properly test the GMVH, an emphasis must be put on VR₀, not merely any individual observed variance ratio. Thus the best empirical evaluations of the hypothesis must include many pairs of d and VR to properly estimate VR₀. In all examples above, there are a few individual cases where VR is not greater than 1. Yet, the expected variance ratio when there is no mean difference is still clearly larger than 1 (practically and significantly so). In the above examples, VR₀ estimates of 1.22, 1.16 and 1.23 were found. In other words, male variance was found to be 16-23% greater, when neither sex had any mean advantage. This clearly supports the GMVH.



I think you should not use the variance ratio, as this metric is not interpretable by intuition. I think people use it because there is a known statistical test for it. The ratio of the standard deviations is better for understanding. So in your results, VR's are 1.16, 1.22, 1.23, mean is 1.20. Sqrt of 1.20 is 1.10, i.e. 10% greater for males. So in terms of IQ, this would correspond to SD's of about 15.7 to 14.3.
But taking VR0 is an egalitarian fault. We know males have higher intelligence by 4-5 points in adulthood, d=0.2 to 0.4 so true VR is not VR0 but about VR0.3 so clearly higher than 1,2...